50 bài tập về Phương pháp quy nạp toán học (có đáp án 2023)

Phương pháp quy nạp toán học và cách giải – Toán lớp 11

1. Lý thuyết

Để chứng minh những mệnh đề liên quan đến số tự nhiên n ∈N* là đúng với mọi n mà không thể thử trực tiếp được thì ta thực hiện theo các bước sau:

Bước 1: Kiểm tra rằng mệnh đề đúng với n = 1.

Bước 2: Giả thiết mệnh đề đúng với một số tự nhiên bất kì n = k, k≥1 (gọi là giả thiết quy nạp).

Bước 3: Ta cần chứng minh mệnh đề đúng với n = k + 1.

Các bước làm bài toán như trên ta gọi là phương pháp quy nạp toán học, hay gọi tắt là phương pháp quy nạp.

Tổng quát:

Xét mệnh đề P(n) phụ thuộc vào số tự nhiên n. Để chứng minh một mệnh đề P(n) đúng với mọi (n0 là số tự nhiên cho trước) thì ta thực hiện theo các bước sau:

Bước 1: Kiểm tra P(n) đúng với n = n0.

Bước 2: Giả sử n≥n0 đúng khi n = k, k≥n0.

Bước 3: Ta cần chứng minh P(n) đúng khi n = k + 1.

Kết luận: Theo nguyên lí quy nạp toán học, ta kết luận rằng P(n) đúng với mọi n≥n0.

2. Các dạng bài tập

Dạng 1. Chứng minh đẳng thức

Phương pháp giải:

Làm theo 3 bước như phần lý thuyết đã nêu.

Ví dụ minh họa:

Ví dụ 1: Chứng minh rằng với mọi số nguyên dương n, ta có:

12+32+52+⋅⋅⋅+2n−12=n4n2−13(1)

Lời giải

Bước 1: Với n = 1, ta có: 1=14.1−13 (đúng). Vậy (1) đúng với n = 1.

Bước 2: Giả sử (1) đúng với n = k. Có nghĩa là ta có:

12+32+52+⋅⋅⋅+2k−12=k4k2−13 2

Bước 3: Ta phải chứng minh (1) đúng với n = k + 1.

Có nghĩa ta phải chứng minh:

12+32+52+⋅⋅⋅+2k−12+2k+12=k+14k+12−13=2k+1k+12k+33

Thật vậy, ta có:

12+32+52+⋅⋅⋅+2k−12+2k+12=k4k2−13+2k+12=k2k+12k−13+2k+12=2k+1k2k−1+32k+13=2k+12k2+5k+33

=2k+1k+12k+33 (điều phải chứng minh).

Vậy (1) đúng khi n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Ví dụ 2: Chứng minh rằng với mọi số nguyên dương n, ta có:

1. 4 + 2. 7 +… + n(3n + 1) = n(n + 1)2 (1)

Lời giải

Bước 1: Với n = 1, ta có: 1. 4 = 1.(1 + 1)2 (đúng). Vậy (1) đúng với n = 1.

Bước 2: Giả sử (1) đúng với n = k. Có nghĩa là ta có: 1. 4 + 2. 7 +… + k(3k + 1) = k(k + 1)2 (2)

Bước 3: Ta phải chứng minh (1) đúng với n = k + 1.

Có nghĩa ta phải chứng minh: 1. 4 + 2. 7 +… + k(3k + 1) + (k + 1)(3k + 4) = (k + 1)(k + 2)2

Thật vậy 1. 4 + 2. 7 +… + k(3k + 1) + (k + 1)(3k + 4)

= k(k + 1)2 + (k + 1)(3k + 4)

= (k + 1)[k(k + 1) + 3k + 4] = (k + 1)(k + 2)2 (điều phải chứng minh).

Vậy (1) đúng khi n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Dạng 2: Chứng minh bất đẳng thức

Phương pháp giải:

Để chứng minh một mệnh đề P(n) > Q(n) phụ thuộc vào số tự nhiên n đúng với mọi (m là số tự nhiên cho trước), ta thực hiện theo hai bước sau:

Bước 1: Chứng minh rằng khi n = m. P(m) > Q(m) luôn đúng

Bước 2: Với k là một số tự nhiên tùy ý, k≥m. Giả sử đúng với n = k, ta được P(k) > Q(k) đúng

Bước 3: Ta sẽ chứng minh đẳng thức đúng khi n = k + 1.

Theo nguyên lí quy nạp toán học, ta kết luận rằng P(n) đúng với mọi số tự nhiên n≥m.

Ví dụ minh họa:

Ví dụ 1: Chứng minh rằng với mọi số nguyên dương n≥3, ta có: 3n > n2 + 4n + 5 (1)

Lời giải

Bước 1: Với n = 3 ta có 33>32+4.3+5⇔27>26 (đúng). Vậy (1) đúng với n = 1.

Bước 2: Giả sử với n=k,k≥3 thì (1) đúng, có nghĩa ta có: 3k > k2 + 4k + 5 (2).

Ta phải chứng minh (2) đúng với n = k + 1

Có nghĩa ta phải chứng minh: 3k + 1 > (k + 1)2 + 4(k + 1) + 5

Thật vậy, nhân hai vế của (1) với 3 ta được: 3.3k > 3.k2 + 12k + 15

3k + 1 > (k2 + 2k + 1) + 4(k + 1) + 5 + (2k2 + 6k + 5)

Vì (2k2+6k+5)>0 ∀k≥3. Vậy 3k + 1 > (k + 1)2 + 4(k + 1) + 5 (đúng).

Vậy (1) đúng với mọi số nguyên dương n≥3.

Ví dụ 2: Chứng minh rằng với mọi số nguyên dương n≥2 ta có:

1n+1+1n+2+⋅⋅⋅+1n+n>1324 (1)

Lời giải

Đặt un=1n+1+1n+2+⋅⋅⋅+1n+(n−1)+1n+n

Bước 1: Với n = 2 ta có u2=12+1+12+2=712>1324 (đúng).

Bước 2: Giả sử với n = k thì (1) đúng, có nghĩa

Ta có: 1k+1+1k+2+⋅⋅⋅+1k+k>1324

Bước 3: Ta phải chứng minh (1) đúng với n = k + 1

Có nghĩa ta phải chứng minh:

1k+2+1k+3+⋅⋅⋅+1k+1+k+1(k+1)+(k+1)>1324

Thật vậy ta có:

uk+1−uk

=1k+2+1k+3+⋅⋅⋅+1k+1+k+1(k+1)+(k+1)−(1k+1+1k+2+⋅⋅⋅+1k+k)

=12k+1+1(k+1)+(k+1)−1k+1=12k+1+12(k+1)−1k+1

=12k+1−12k+2>0 (đúng).

Vậy uk+1>uk>1324 (đúng). Vậy (1) đúng với n = k + 1.

Vậy (1) đúng với mọi số nguyên dương n≥2.

Dạng 3: Chứng minh sự chia hết

Phương pháp giải:

Làm theo 3 bước như phần lý thuyết đã nêu.

Chú ý một số dấu hiệu chia hết

– Dấu hiệu chia hết cho 2: các số có chữ số tận cùng là 0, 2, 4, 6, 8.

– Dấu hiệu chia hết cho 5: các số có chữ số tận cùng là 0 hoặc 5.

– Dấu hiệu chia hết cho 3: các số có tổng các chữ số chia hết cho 3.

– Dấu hiệu chia hết cho 9: các số có tổng các chữ số chia hết cho 9.

– Dấu hiệu chia hết cho 4: hai chữ số tận cùng tạo thành 1 số chia hết cho 4.

– Dấu hiệu chia hết cho 6: các số vừa chia hết cho 2 vừa chia hết cho 3.

– Dấu hiệu chia hết cho 8: ba chữ số tận cùng tạo thành 1 số chia hết cho 8.

– Dấu hiệu chia hết cho 10: chữ số tận cùng bằng 0.

– Tích của hai số tự nhiên liên tiếp luôn chia hết cho 2.

– Tích của ba số tự nhiên liên tiếp luôn chia hết cho 2, 3 và 6.

– Tích của bốn số tự nhiên liên tiếp luôn chia hết cho 2, 3, 4, 6 và 8.

– Tính chất của sự chia hết:

+ Nếu hai số a và b đều chia hết cho m, thì tổng (a + b) và hiệu (a – b) chia hết cho m.

+ Nếu mỗi số ai⋮mi,i=1,2,…,n thì tích a1a2…an⋮m1m2…mn.

Ví dụ minh họa:

Ví dụ 1: Chứng minh rằng với mọi n∈ℕ*thì n3 + 2n chia hết cho 3.

Lời giải

Đặt P(n) = n3 + 2n.

Bước 1: Với n = 1, ta có P(1)=13+2.1=3⋮3. Suy ra P(n) đúng với n = 1.

Bước 2: Giả sử mệnh đề đúng khi n=k≥1, tức là: P(k)=k3+2k⋮3

Bước 3: Ta cần chứng minh mệnh đề đúng khi n = k + 1

Tức là chứng minh: P(k+1)=(k+1)3+2(k+1)⋮3.

Thật vậy:

P(k + 1) = k3 + 3k2 + 3k + 1 + 2k + 2

= k3 + 3k2 + 5k + 3

= (k3 + 2k) + 3(k2 + k + 1)

= P(k) + 3(k2 + k + 1).

Mà P(k)⋮3 và 3(k2+k+1)⋮3 nên P(k+1)⋮3⇒mệnh đề đúng khi n = k + 1.

Vậy theo nguyên lí quy nạp toán học ta có mệnh đề đúng với mọi n∈ℕ*.

Ví dụ 2: Chứng minh rằng với mọi n∈ℕ* thì 4. 6n + 5n – 4 chia hết cho 5.

Lời giải

Đặt P(n) = 4. 6n + 5n – 4.

Bước 1: Với n = 1, ta có P(1)=4.61+51−4=25⋮5. Suy ra mệnh đề đúng với n = 1.

Bước 2: Giả sử mệnh đề đúng khi , tức là: P(k)=4.6k+5k−4⋮5.

Bước 3: Ta cần chứng minh mệnh đề đúng khi n = k + 1

Tức là chứng minh: P(k+1)=4.6k+1+5k+1−4  ⋮ 5.

Thật vậy:

P(k + 1) = 4. 6k+1 + 5k+1 – 4

= 4.6k.6 + 5k.5 – 4

= 24.6k + 5.5k – 4

= 6(4.6k + 5k – 4) – 5k + 20

= 6P(k) – 5k + 20

Mà 6P(k)⋮55k⋮520⋮5 nên P(k+1)⋮5⇒mệnh đề đúng khi n = k + 1.

Vậy theo nguyên lí quy nạp toán học ta có mệnh đề đúng với mọi n∈ℕ*.

Dạng 4: Quy nạp trong hình học

Phương pháp giải:

Làm theo 3 bước như phần lý thuyết đã nêu.

Ví dụ minh họa:

Ví dụ 1: Chứng minh rằng tổng các góc trong của một đa giác lồi n cạnh n≥3 là: (n – 2)1800.

Lời giải

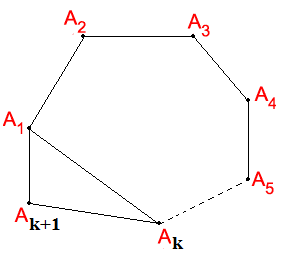
Đặt S(n) = (n – 2)1800.

Bước 1: Với n = 3, ta có S(3) = 1800. Suy ra mệnh đề đúng với n = 1.

Bước 2: Giả sử mệnh đề đúng khi n=k≥3, tức là: S(k) = (k – 2)1800.

Bước 3: Ta cần chứng minh mệnh đề đúng khi n = k + 1

Tức là chứng minh: S(k + 1) = (k – 1)1800.

Thật vậy: ta tách đa giác (k + 1) cạnh thành đa giác k cạnh và tam giác A1AkAk+1 bằng cách nối đoạn A1Ak. Khi đó tổng các góc trong của đa giác lồi (k + 1) cạnh bằng tổng các góc trong của đa giác lồi k cạnh cộng với tổng ba góc trong của tam giác A1AkAk+1.

Tức là: S(k + 1) = S(k) + 1800 = (k – 2)1800 + 1800 = (k – 1)1800

Do đó mệnh đề đúng khi n = k + 1.

Vậy theo nguyên lí quy nạp toán học ta có mệnh đề đúng với mọi n∈ℕ*;n≥3.

Ví dụ 2: Chứng minh rằng số đường chéo của một đa giác lồi n cạnh n≥4 là: nn−32.

Lời giải

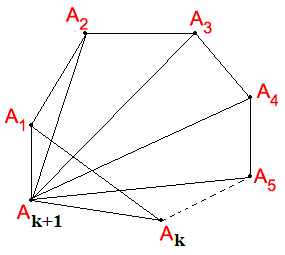
Đặt S(n)=nn−32.

Bước 1: Khi n = 4, ta có S(4) = 2. Suy ra mệnh đề đúng với n = 4.

Bước 2: Giả sử mệnh đề đúng khi n=k≥4, tức là: S(k)=kk−32.

Bước 3: Ta cần chứng minh mệnh đề đúng khi n = k + 1.

Tức là chứng minh: S(k+1)=k+1k−22.

Thật vậy: ta tách đa giác (k + 1) cạnh thành đa giác k cạnh và tam giác A1AkAk+1 bằng cách nối đoạn A1Ak.

Khi đó trừ đi đỉnh đỉnh Ak + 1 và 2 đỉnh kề với nó là A1Ak thì ta còn lại (k + 1) – 3 = k – 2 đỉnh, tương ứng với (k – 2) đường chéo kẻ từ đỉnh Ak+1 cộng với đường chéo A1Ak thì ta có số đường chéo của đa giác (k + 1) cạnh là:

S(k+1)=kk−32+(k−2)+1=kk−32+k−1=k2−k−22=k+1k−22

Do đó mệnh đề đúng khi n = k + 1.

Vậy theo nguyên lí quy nạp toán học ta có mệnh đề đúng với mọi n∈ℕ*,n≥4.

3. Bài tập tự luyện

Bài tập trắc nghiệm

Câu 1. Một học sinh chứng minh mệnh đề “8n + 1 chia hết cho 7, với mọi số tự nhiên n khác 0” (*) như sau:

– Giả sử (1) đúng với n = k, tức là 8k + 1 chia hết cho 7.

– Ta có: 8k + 1 + 1 = 8(8k + 1) – 7, kết hợp với giả thiết 8k + 1 chia hết cho 7 nên suy ra được 8k + 1 + 1 chia hết cho 7. Vậy đẳng thức (1) đúng với mọi n∈ℕ*.

Khẳng định nào sau đây là đúng?

A. Học sinh trên chứng minh đúng.

B. Học sinh chứng minh sai vì không có giả thiết qui nạp.

C. Học sinh chứng minh sai vì không dùng giả thiết qui nạp.

D. Học sinh không kiểm tra bước 1 (bước cơ sở) của phương pháp qui nạp.

Câu 2. Cho Sn=11.2+12.3+13.4+…+1n.n+1 với n∈ℕ*. Mệnh đề nào sau đây đúng?

A. Sn=n−1n.

B. Sn=nn+1.

C. Sn=n+1n+2.

D. Sn=n+2n+3.

Câu 3. Cho Sn=11.3+13.5+…+12n−1.2n+1 với n∈ℕ*.Mệnh đề nào sau đây đúng?

A. Sn=n−12n−1.

B. Sn=n2n+1.

C. Sn=n3n−2.

D. Sn=n+22n+5.

Câu 4. Với mọi n∈ℕ*., hệ thức nào sau đây là sai?

A. 1+2+…+n=nn+12

B. 1+3+5+…+2n−1=n2

C. 12+22+…+n2=nn+12n+16

D. 22+42+62+⋯+2n2=2nn+12n+16

Câu 5. Cho Pn=1−1221−132…1−1n2 với n≥2 và n∈ℕ. Mệnh đề nào sau đây đúng?

A. P=n+1n+2.

B. P=n−12n.

C. P=n+1n.

D. P=n+12n.

Đáp án

1

2

3

4

5

D

B

B

D

D

Bài tập tự luận

Câu 6. Chứng minh rằng với mọi số nguyên dương n, ta có:

1.2+2.3+3.4+⋅⋅⋅+n(n+1)=n(n+1)(n+2)3

Câu 7. Chứng minh rằng với mọi số nguyên dương n, ta có:

1.2 + 2.5 + 3.8 + …+ n(3n – 1) = n2(n+1).

Câu 8. Chứng minh rằng với mọi số nguyên dương n, ta có:

22+42+62+⋅⋅⋅+2n2=2nn+12n+13

Câu 9. Chứng minh rằng với mọi số nguyên dương n≥2, ta có:

1−141−191−116…1−1n2=n+12n

Câu 10. Chứng minh rằng với mọi số nguyên dương n, ta có:

13+23+33+⋅⋅⋅+n3=n2n+124.

Câu 11. Chứng minh rằng với mọi số nguyên dương n≥5, ta có: 2n > n2.

Câu 12. Chứng minh rằng với mọi số nguyên dương n≥3, ta có: 2n > 2n +1.

Câu 13. Chứng minh rằng với mọi số nguyên dương n≥4, ta có: 3n-1 > n(n +2).

Câu 14. Chứng minh rằng với mọi số nguyên dương n thì n3 + 11n chia hết cho 6.

Câu 15. Chứng minh rằng với mọi số nguyên dương n thì 4n + 15n – 1 chia hết cho 9.

Xem thêm các dạng bài tập Toán lớp 9 có đáp án và lời giải chi tiết khác:

Dãy số và cách giải các dạng bài tập

Cấp số cộng và cách giải các dạng bài tập

Cấp số nhân và cách giải các dạng bài tập

Giới hạn của dãy số và cách giải bài tập

Giới hạn của hàm số và cách giải bài tập